Démontrer qu'un quadrilatère est un rectangle ou un carré

Les rectangles et les carrés sont des quadrilatères particuliers. Un quadrilatère étant donné, quelle(s) propriété(s) suffit-il de connaître pour pouvoir affirmer qu'il s'agit d'un rectangle ou d'un carré ?

1. Démontrer qu'un quadrilatère est un rectangle

Un rectangle est un quadrilatère qui a quatre angles droits.

1.1. Avec les côtés et un angle

Si un quadrilatère est un parallélogramme et a un angle droit au moins, alors ce quadrilatère est un rectangle. Autrement dit, les quatre angles du quadrilatère considéré sont droits.

Exemple : sur la figure 1, AB = CD = 3 cm et BC = AD = 2 cm, donc le quadrilatère ABCD est un parallélogramme puisque ses côtés opposés ont deux à deux la même longueur. De plus, l'angle Â est droit ; on peut alors affirmer que ABCD est un rectangle.

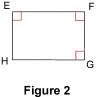
1.2. Avec trois angles

Si un quadrilatère a trois angles droits, alors c'est un rectangle. Autrement dit, le quadrilatère considéré a nécessairement quatre angles droits.

Exemple : sur la figure 2, par hypothèse les angles  , et sont droits ; donc le quadrilatère EFGH est un rectangle.

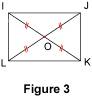
1.3. Avec les diagonales

Si les diagonales d'un quadrilatère ont le même milieu et la même longueur, alors ce quadrilatère est un rectangle.

Exemple : sur la figure 3, IO = OK = JO = OL ; les diagonales du quadrilatère IJKL ont donc le même milieu O et la même longueur, égale à 2OI par exemple ; donc IJKL est un rectangle.

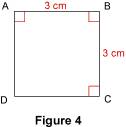
2. Démontrer qu'un quadrilatère est un carré

On peut commencer par démontrer que le quadrilatère est un rectangle ou un losange.

2.1. En partant d'un rectangle

Si un rectangle a deux côtés consécutifs de même longueur, alors c'est un carré.

Exemple : sur la figure 4, le quadrilatère ABCD est un rectangle puisqu'il a trois angles droits ; de plus, AB = BC = 3 cm ; ABCD est donc un carré.

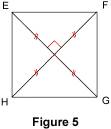
Si un rectangle a ses diagonales perpendiculaires, alors c'est un carré.

Exemple : sur la figure 5, en se référant au codage, on voit que le quadrilatère EFGH est un rectangle puisque ses diagonales ont le même milieu et la même longueur ; de plus, ses diagonales sont perpendiculaires ; EFGH est donc un carré.

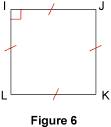
2.2. En partant d'un losange

Si un losange a un angle droit au moins, alors c'est un carré.

Exemple : sur la figure 6, en se référant au codage, on voit que le quadrilatère IJKL est un losange puisqu'il a quatre côtés de même longueur ; de plus, l'angle  est droit ; IJKL est donc un carré.

Si un losange a ses diagonales de même longueur, alors c'est un carré.

Exemple : sur la figure 7, en se référant au codage, on voit que le quadrilatère EFGH est un losange puisque ses diagonales ont le même milieu et sont perpendiculaires ; comme de plus elles ont la même longueur, EFGH est un carré.