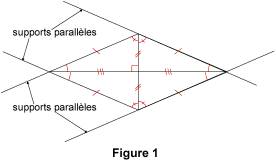
Démontrer qu'un quadrilatère est un losange

Les losanges sont des quadrilatères particuliers. Un quadrilatère étant donné, quelle(s) propriété(s) suffit-il de connaître pour pouvoir affirmer qu'il s'agit d'un losange ?

1. Rappels sur les losanges

Un losange est un quadrilatère dont les quatre côtés ont la même longueur.

Les propriétés d'un losange sont symbolisées sur la figure 1.

On voit par exemple que les diagonales d'un losange sont des axes de symétrie.

2. Démontrer qu'un quadrilatère est un losange

2.1. Avec les côtés

D'après la définition précédente, si un quadrilatère a quatre côtés de même longueur, alors c'est un losange.

Exemple : sur la figure 2, AB = BC = CD = DA = 3 cm ; donc ABCD est un losange.

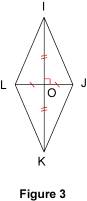
Remarque : si un parallélogramme a deux côtés consécutifs de même longueur, alors c'est un losange (puisqu'on sait que les côtés opposés d'un parallélogramme ont deux à deux la même longueur).

2.2. Avec les diagonales

Si les diagonales d'un quadrilatère ont le même milieu et sont perpendiculaires, alors ce quadrilatère est un losange.

Exemple : Sur la figure 3, IO = OK et JO = OL ; donc les diagonales du quadrilatère IJKL ont le même milieu O.

De plus, ces diagonales sont perpendiculaires ; on peut alors affirmer que IJKL est un losange.

Remarque : il revient au même d'énoncer :

si un quadrilatère admet les supports de ses diagonales comme axes de symétrie, alors c'est un losange ;

si les supports des diagonales d'un quadrilatère sont les bissectrices de ses angles, alors ce quadrilatère est un losange ;

si un parallélogramme a des diagonales perpendiculaires, alors c'est un losange.