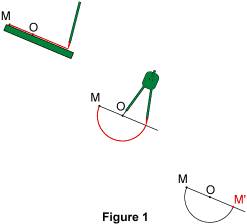
Construire le symétrique d'une figure par rapport à un point

L'image d'une figure par symétrie centrale de centre O est une figure superposable à la première par rotation d'un demi-tour autour de O.

Comment construit-on ce symétrique dans le cas de figures usuelles. Qu'en est-il pour les autres cas ?

1. Construire le symétrique d'un point

Soit O un point. Le symétrique par rapport à O d'un point M est le point M' tel que O soit le milieu du segment [MM']. La figure 1 montre une construction de M' à la règle et au compas.

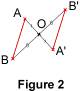
Remarque : le symétrique de O par rapport à O est lui-même.

2. Construire le symétrique d'une figure usuelle

On considère une symétrie centrale de centre O.

2.1. Le symétrique d'un segment

Le symétrique du segment [AB] est le segment [A'B'] tel que A' est le symétrique de A et B' le symétrique de B par rapport à O.

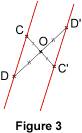
2.2. Le symétrique d'une droite

Le symétrique d'une droite (CD) est une droite (C'D') tel que C' est le symétrique de C et D' le symétrique de D par rapport à O.

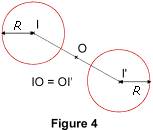
2.3. Le symétrique d'un cercle

Le symétrique d'un cercle de centre I et de rayon R est un cercle de centre I' et de rayon R tel que I' est le symétrique de I par rapport à O.

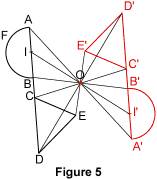
3. Construire le symétrique d'une figure particulière

Pour construire le symétrique de la figure F, on peut :

construire les symétriques A', D' et E' des points A, D et E ;
tracer les segments [A'D'] et [D'E'] ;

tracer les droites (IO), (BO) et (CO), ce qui donne I', B' et C' ;
terminer en traçant le segment [E'C'] et le demi-cercle.