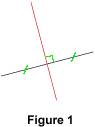
Construire le cercle circonscrit à un triangle

Le cercle circonscrit à un triangle est l'unique cercle qui contient les trois sommets de ce triangle. Comment le construire ? Où est son centre ?

1. Définitions et propriétés

1.1. Rappels sur les médiatrices

La médiatrice d'un segment est la droite qui est perpendiculaire à ce segment et qui passe par son milieu.

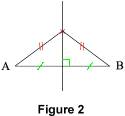
Propriété : soit [AB] un segment,

tout point de la médiatrice de [AB] est équidistant de A et de B ;

les points équidistants de A et de B sont sur la médiatrice de [AB].

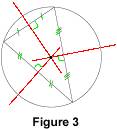
Remarque : les médiatrices d'un triangle sont les médiatrices des côtés de ce triangle. Un triangle a donc trois médiatrices.

1.2. Une nouvelle propriété

Les trois médiatrices d'un triangle sont concourantes en un point qui est équidistant des trois sommets.

En effet, soit ABC un triangle et soit O le point d'intersection des médiatrices des côtés [AB] et [BC].

D'après la propriété de la médiatrice, O est équidistant de A et de B, et O est équidistant de B et de C. Donc O est équidistant de A et de C, et O est sur la médiatrice de [AC].

On en déduit que les trois médiatrices sont concourantes en O. De plus, nous avons vu que O est équidistant de A, B et C.

1.3. Le cercle circonscrit

D'après la propriété précédente, le point de concours O des trois médiatrices d'un triangle ABC est équidistant des trois sommets du triangle. Le point O est donc le centre d'un cercle qui passe par les trois sommets de ABC.

Ce cercle s'appelle le cercle circonscrit au triangle ABC.

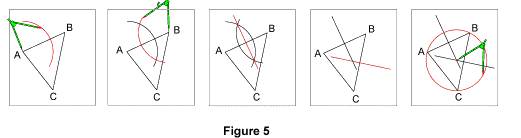
Remarque : il n'y a qu'un seul point équidistant de A, B et C puisque les trois médiatrices sont concourantes ; il n'y a donc qu'un seul cercle passant par les trois sommets d'un triangle ABC.

2. Construction du cercle circonscrit

Il suffit de tracer les médiatrices de deux côtés d'un triangle ; d'après la propriété des médiatrices du triangle, la médiatrice du troisième côté passe nécessairement par ce point. C'est le centre du cercle circonscrit au triangle.