Compléter un tableau de proportionnalité

Dans un tableau de proportionnalité, les nombres de la 2e ligne sont respectivement égaux à k fois les nombres de la 1re ligne (k désignant le coefficient de proportionnalité).

Si l’on doit compléter un tableau de proportionnalité, deux cas se présentent :

le coefficient de proportionnalité k est connu ;

le coefficient de proportionnalité k n’est pas connu.

Comment procéder dans chacun des cas ?

1. Compléter un tableau de proportionnalité

1.1. Le coefficient de proportionnalité est connu

Exemple : on veut compléter le tableau de proportionnalité ci-dessous, sachant que le coefficient de proportionnalité est égal à 0,25.

1re colonne : on multiplie 6 par le coefficient de proportionnalité ; 6 × 0,25 = 1,5.

2e colonne : on multiplie de même ; 1,2 × 0,25 = 0,3.

3e colonne : soit x le nombre cherché ; on a x × 0,25 = 28, donc x = 28 ÷ 0,25 = 112.

On obtient alors le tableau ci-dessous :

Remarque : dans un tableau de proportionnalité, tout nombre de la 1re ligne est égal au nombre correspondant de la 2e ligne divisé par k (k désignant le coefficient de proportionnalité, supposé non nul).

1.2. Le coefficient de proportionnalité n’est pas connu

Exemple 1 : on veut compléter le tableau de proportionnalité ci-dessous :

On commence par calculer le coefficient de proportionnalité k. Cela est possible quand on connaît les deux nombres d’une même colonne.

Avec les nombres de la 1re colonne, on peut écrire : 8 × k = 36 ; donc k = 36 ÷ 8 = 4,5.

On procède alors comme dans le paragraphe 1 : 52 × 4,5 = 234 et 15,3 ÷ 4,5 = 3,4.

On obtient alors le tableau ci-dessous :

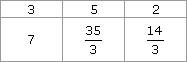
Exemple 2 : on veut compléter le tableau de proportionnalité ci-dessous :

Le coefficient de proportionnalité k est tel que : 3 ×  k = 7 ; donc .

On doit utiliser une forme fractionnaire pour écrire k (car la division 7 ÷ 3 ne tombe pas juste).

On calcule alors les deux nombres manquants : et .

On obtient le tableau ci-dessous :

2. Calculer une quatrième proportionnelle

12 litres de grand vin coûtent 294 € ; combien coûtent 8 litres de ce vin ?

Nous allons résoudre ce problème en appliquant trois méthodes différentes ; il s’agit en réalité de trois présentations différentes.

2.1. Appliquer la « règle de trois »

12 L coûtent 294 €.

1 L coûte  € (12 fois moins que 12 L).

8 L coûtent  € (8 fois plus que 1 L).

donc 8 L de vin coûtent 196 €.

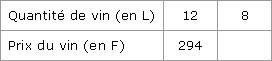
2.2. Chercher le quatrième nombre dans un tableau de proportionnalité

Le prix du vin est proportionnel à la quantité de vin. Le prix cherché s’obtient en déterminant le nombre manquant du tableau de proportionnalité suivant :

On calcule le coefficient de proportionnalité : k = 294 ÷ 12 = 24,5.

Le nombre manquant dans le tableau est : 8 × 24,5, soit 196, donc 8 L de vin coûtent 196 €.

Remarque : le coefficient de proportionnalité 24,5 est le prix d’un litre de vin (en €).

3. Utiliser les « produits en croix »

On commence comme dans la deuxième méthode. Appelons x le nombre manquant dans le tableau. Deux « produits en croix » dans un tableau de proportionnalité sont égaux ; donc :

12 × x = 294 × 8
12x = 2 352
x = 2 352 ÷ 12
x = 196

8 L de vin coûtent 196 €.