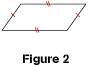
Caractériser et construire un parallélogramme

Les parallélogrammes sont des quadrilatères.

Quelles sont leurs propriétés et comment peut-on les tracer ?

1. Caractériser un parallélogramme

Un quadrilatère est un parallélogramme…

si ses côtés opposés sont parallèles deux à deux (1)

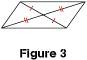
ou bien si ses côtés opposés ont deux à deux même longueur (le quadrilatère n'étant pas croisé) (2)

ou bien si ses diagonales ont le même milieu, autrement dit, s'il a un centre de symétrie (3)

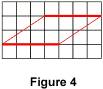
ou bien s'il a deux côtés parallèles de même longueur (le quadrilatère n'étant pas croisé) (4).

Remarque : d'après cette dernière propriété, il est facile de dessiner un parallélogramme sur une feuille quadrillée ; il suffit de tracer deux segments sur des lignes parallèles en comptant le même nombre de carreaux, puis de joindre les extrémités de ces segments.

2. Construire un parallélogramme

2.1. En utilisant la propriété (1)

On donne trois points A, B et D non alignés. Il s'agit de construire à la règle et à l'équerre le point C tel que ABCD soit un parallélogramme et de tracer ce parallélogramme.

On trace la parallèle à la droite (AB) passant par le point D.

On trace la parallèle à la droite (AD) passant par le point B.

C est le point d'intersection des deux droites tracées.

2.2. En utilisant la propriété (2)

On donne trois points E, F et H non alignés. Il s'agit de construire au compas le point G tel que EFGH soit un parallélogramme et de tracer ce parallélogramme.

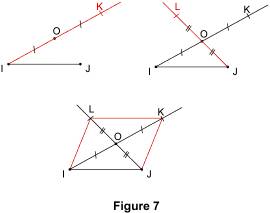
On repère approximativement la position du point G cherché.

On trace un arc de cercle de centre H et de rayon EF (le compas est donc réglé avant le tracé sur la longueur EF) ; on trace cet arc vers la position repérée.

On trace un arc de cercle de centre F et de rayon EH qui coupe l'arc précédent.

G est le point d'intersection des deux arcs de cercle.

2.3. En utilisant la propriété (3)

On donne trois points I, J et O non alignés. Il s'agit de construire à la règle et au compas les points K et L tel que IJKL soit un parallélogramme de centre O.

On construit le symétrique K du point I par rapport au point O.

On construit le symétrique L du point J par rapport à O.

On peut tracer le parallélogramme IJKL.