Calculer le volume d'un prisme droit ou d'un cylindre de révolution

Les aires latérales d’’un prisme droit et d’’un cylindre de révolution s’’expriment à l’’aide de la même formule : A = P × h. Comment peut-on calculer leur volume ?

1. Volume d’un prisme droit

1.1. Formule

Le volume V d’un prisme droit de hauteur h et ayant une base d’aire B est donné par la formule : V = B × h.

Pour appliquer cette formule, h, B et V doivent être exprimés dans des unités correspondantes ;
par exemple : h en cm, B en cm2 et V en cm3.

1.2. Exemple

On veut calculer le volume des prismes droits représentés sur la figure 2.

Prisme P1 : ses bases sont trapézoïdales (sur la figure, le prisme n’’est pas posé sur une base).

On calcule l’’aire d’’un trapèze de base avec la formule où B = 2 m, b = 1 m et h

 = 12 m ; , donc l’’aire de base du prisme est égale à 18 m2.

On calcule alors le volume du prisme avec la formule V = B × h où B = 18 m2 et h = 25 m ; 18 × 25 = 450, donc le volume du prisme est égal à 450 m3

Prisme P2 : une base du prisme, en forme de U, est représentée ci-dessus

On peut calculer son aire B par différence : B = aire (ABCD) - aire (EFGH) = 16 cm2 - 10,5 cm2 = 5,5 cm2
(4 ×4 = 16 ; 3 × 3,5 = 10,5 et 16 - 10,5 = 5,5).

On calcule alors le volume du prisme avec la formule V = B × h où B = 5,5 cm2 et h = 2 m = 200 cm ; 5,5 × 200 = 1 100, donc le volume du prisme est égal à 1 100 cm3.

2. Volume d’’un cylindre de révolution

2.1. Formules

Le volume V d’’un cylindre de révolution de hauteur h et de rayon R est donné par la formule :
V =   × R × R × h ( est le nombre pi, environ 3,14).

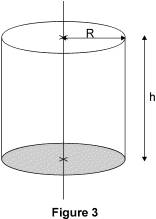
Si l’’on appelle B l’’aire de base, c’’est-à-dire l’aire ’d’un disque de rayon R, on a : B =   × R × R, et la formule précédente devient : V = B × h.

Pour appliquer ces formules, h, R, B et V doivent être exprimés dans des unités correspondantes ; par exemple :

h en cm, R en cm, B en cm2 et V en cm3.

2.2. Exemple

Calculons le volume d’’un cylindre de révolution de rayon 5 cm et de hauteur 10 cm :

 × 5 × 5 = 25  ; donc l’’aire de base B est égale à 25  cm2.

25  × 10 = 250  ; donc le volume V du cylindre est égal à 250  cm3, soit environ 785 cm3.