Calculer l'aire d'un parallélogramme

L'aire d'un rectangle de longueur L et de largeur l est donnée par la formule : A = L × l.

Par quelle formule similaire peut-on calculer l'aire d'un parallélogramme et quelles sont les applications directes de cette formule ?

1. La formule

Dans un parallélogramme, on peut choisir deux côtés opposés comme bases. Il est commode de désigner par le même mot (base) la longueur de ces côtés.

Ces bases étant choisies, on peut considérer la hauteur relative à ces bases.

Par exemple, on peut considérer que le parallélogramme représenté sur la figure 1 a une base égale à 10 cm ; dans ce cas sa hauteur est égale à 4 cm.

On peut aussi considérer qu'il a une base égale à 5 cm ; sa hauteur est alors égale à 8 cm.

L'aire A d'un parallélogramme de base b et de hauteur h est donnée par la formule : A = b × h.

Pour appliquer cette formule, b et h doivent être exprimés dans la même unité ; A sera alors exprimée dans l'unité correspondante. Par exemple, si b et h sont exprimés en cm, A sera exprimée en cm².

Remarque : l'aire d'un parallélogramme équivaut à celle d'un rectangle de dimensions b et h.

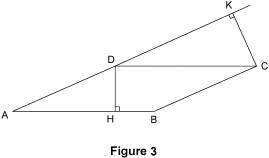
2. Exemples d'application

2.1 Exemple 1

Calculons l'aire du parallélogramme de la figure 1 en reprenant les hypothèses ci-dessus :

Hypothèse 1 : b = 10 cm ; h = 4 cm ; 10 × 4 = 40 ; l'aire du parallélogramme est égale à 40 cm2 ;

Hypothèse 2 : b = 5 cm ; h = 8 cm ; 5 × 8 = 40 ; l'aire du parallélogramme est égale à 40 cm2.
Bien sûr, on retrouve le même résultat.

2.2 Exemple 2

Dans cet exemple, on utilise l'aire d'un parallélogramme pour calculer la longueur d'un de ses côtés.

Sur la figure 4, ABCD est un parallélogramme. On donne AD = 4 cm, DH = 1,6 cm et CK = 2 cm. Calculer AB.

Calculons l'aire A du parallélogramme de deux façons :

en prenant b = AD = 4 cm et h = CK = 2 cm : 4 × 2 = 8 ; donc A = 8 cm2 ;
en prenant b = AB = x cm et h = DH = 1,6 cm : x × 1,6 = 1,6x ; donc A = 1,6x cm2.

Les deux façons doivent donner le même résultat, donc : 1,6x = 8 ; d'où : x = 8 : 1,6 = 5.
On a trouvé : AB = 5 cm.