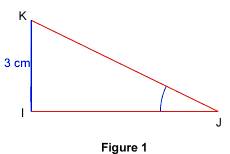
Calculer la longueur d'un côté ou un angle dans un triangle rectangle

Pour calculer un côté d'un triangle rectangle connaissant les deux autres, on a recours au théorème de Pythagore. Si on connaît seulement un côté et un angle aigu, on peut utiliser le sinus, le cosinus ou la tangente de cet angle.

1. Calcul de la longueur d'un côté

Il s'agit de calculer la longueur d'un côté d'un triangle rectangle connaissant la longueur d'un autre côté et la mesure d'un de ses angles aigus. Il suffit pour cela de caractériser le côté connu et le côté inconnu par rapport à l'angle dont la mesure est connue. On saura ainsi quel rapport trigonométrique on doit utiliser : le sinus, le cosinus ou la tangente.

Prenons un exemple.

Énoncé : soit IJK un triangle rectangle en I tel que IK = 3 cm et  = 26°. On veut calculer KJ et IJ à 0,01 cm près.

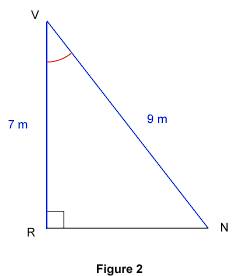
Résolution : on connaît IK qui est la longueur du côté opposé à , et on cherche KJ qui est la longueur de l'hypoténuse du triangle ; on va donc utiliser le sinus de l'angle  . En effet, dans

un triangle rectangle, le sinus d'un angle aigu est égal au rapport  .

On écrit : sin  , soit sin 26° =  , et on en déduit que KJ =  .

D'où, à l'aide d'une calculatrice, on a : KJ   6,84 cm.

Calculons IJ : on connaît IK qui est la longueur du côté opposé à , et on cherche IJ qui est la longueur du côté adjacent à  ; on va donc utiliser la tangente de l'angle  . En effet, dans un

triangle rectangle, la tangente d'un angle aigu est égale au rapport  .

On écrit : tan  , soit tan 26° =  , et on en déduit que IJ =  .

D'où, à l'aide d'une calculatrice : IJ   6,15 cm.

2. Calcul d'un angle

Il s'agit de calculer la mesure d'un angle d'un triangle rectangle, connaissant les longueurs de deux de ses côtés. Il suffit pour cela de caractériser les deux côtés connus par rapport à l'angle dont la mesure est à calculer ; on saura ainsi quel rapport trigonométrique on doit utiliser (le sinus, le cosinus ou la tangente).

Prenons un exemple.

Énoncé : soit NRV un triangle rectangle en R tel que RV = 7 m et NV = 9 m.

On veut calculer la mesure de l'angle  arrondie à 0,1° près.

Résolution : RV est la longueur du côté adjacent à l'angle  , et NV est la longueur de l'hypoténuse du triangle ; on va donc utiliser le cosinus de l'angle  . En effet, dans un triangle

rectangle, le cosinus d'un angle aigu est égal au rapport  .

On écrit cos  , soit cos  et on en déduit, à l'aide d'une calculatrice, que 38,9°.