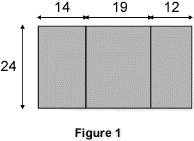
Appliquer les règles de distributivité

Pour calculer astucieusement A = 57 × 968 + 43 × 968, il suffit d'appliquer une règle de distributivité qui permet d'écrire : A = (57 + 43) × 968 = 100 × 968. On trouve alors 96 800.

Quelles sont les différentes règles de distributivité et quand les utiliser ?

1. Règles de distributivité

Dans les deux paragraphes suivants, a, b et k désignent des nombres quelconques.

1.1 Distributivité de la multiplication par rapport à l'addition

Il s'agit de la règle : k × (a + b) = k × a + k × b

On peut l'écrire plus simplement : k(a + b) = ka + kb

Exemple : 2 × (3 + 4) = 2 × 3 + 2 × 4

On peut vérifier que : 2 × (3 + 4) = 2 × 7 = 14

et que : 2 × 3 + 2 × 4 = 6 + 8 = 14.

Remarque : on a aussi : (a + b) × k = a × k + b × k et donc : (a + b)k = ak + bk = ka + kb = k(a + b)

1.2 Distributivité de la multiplication par rapport à la soustraction

Il s'agit de la règle : k × (a – b) = k × a – k × b

On peut l'écrire plus simplement : k(a – b) = ka – kb

Exemple : 3 × (5 – 2) = 3 × 5 - 3 × 2

Remarque : on a aussi : (a – b) × k = a × k – b × k

et donc : (a – b)k = ak – bk = ka – kb = k(a – b).

1.3 Généralisation

Les formules précédentes se généralisent à un nombre quelconque de termes dans les parenthèses.

Exemple : 2 × (3 + 4 – 5) = 2 × 3 + 2 × 4 – 2 × 5

2. Exemples d'application

2.1. Calculer mentalement

Exemple 1 : on veut calculer : 25 × 11 ; 25 × 21 et 25 × 31.

On peut procéder ainsi :

25 × 11 = 25 × (10 + 1) = 25 × 10 + 25 × 1 = 250 + 25 = 275

De même :

25 × 21 = 25 × 20 + 25 = 500 + 25 = 525

25 × 31 = 25 × 30 + 25 = 750 + 25 = 775

Exemple 2 : on veut calculer 24 × 9 ; 24 × 19 et 24 × 29.

On peut procéder ainsi :

24 × 9 = 24 × (10 – 1) = 24 × 10 – 24 × 1 = 240 – 24 = 216

De même :

24 × 19 = 24 × (20 – 1) = 24 × 20 – 24 × 1 = 480 – 24 = 456

24 × 29 = 24 × (30 – 1) = 24 × 30 – 24 × 1 = 720 – 24 = 696

2.2 Calculer l'aire de la surface latérale d'un prisme droit

La figure 1 montre le patron de la surface latérale d'un prisme droit. L'unité de longueur est le centimètre.

Pour calculer l'aire de cette surface, on pourrait effectuer le calcul suivant :

24 × 14 + 24 × 19 + 24 × 12

Cela reviendrait à additionner les aires des trois rectangles.

Il est cependant plus simple d'effectuer le calcul :

24 × (14 + 19 + 12) = 24 × 45 = 1 080

On trouve ainsi que l'aire de cette surface est égale à 1 080 cm2.

Remarque : (14 + 19 + 12) est la mesure en centimètres du périmètre d'une base du prisme.

2.3 Calculer l'aire d'une couronne circulaire

On veut calculer l'aire de la couronne circulaire coloriée sur la figure ci-dessous. L'unité de longueur est le centimètre. L'unité d'aire est le centimètre carré.

L'aire de cette couronne est égale à la différence entre l'aire du grand disque de rayon 3 cm et l'aire du petit disque de rayon 2 cm. On a :

aire du grand disque :  × 32 =   × 3 × 3 = 9  ;

aire du petit disque :  × 22 =   × 2 × 2 = 4  ;

aire de la couronne : 9  - 4  = (9 – 4)  = 5 .

L'aire de la couronne est donc égale à 5  cm2.

En prenant    3,14, on trouve une aire environ égale à 15,7 cm2.

Remarque : plus généralement, l'aire d'une couronne circulaire limitée par deux cercles concentriques de rayons respectifs R et r est égale à R² –  r², c'est-à-dire (R² – r²).